|
农地征用补偿的期权价格模型
湖南新三星房地产土地评估咨询有限公司
李福林、吴武成
摘要:我国《土地管理法》中规定,国家出于公共利益及经济发展需要,当涉及占用村集体组织农业用地时,须先由国家征收转为全民所有性质的建设用地,再由国家以划拨或出让方式供给新的用地方。在农地征收货币补偿方面,给出了一个适当合理的量化方法显然具有积极的现实意义。因此我们尝试运用金融衍生工具的期权定价原理,建立征收农地的期权价格补偿模型。
关键词:农地 征收 补偿 期权 价格模型
一、概述
我国《土地管理法》中规定,国家出于公共利益及经济发展需要,当涉及占用村集体组织农业用地时,须先由国家征收转为全民所有性质的建设用地,再由国家以划拨或出让方式供给新的用地方。在农地征用阶段,国家采用被征地年产值倍数对所征地进行货币补偿,主要包括土地补偿费和安置补助费,二者之和的最高标准为补征地前三年平均产值的30倍。农地按所产物大致分为粮食、蔬菜、经济作物、园林、水产养殖、畜牧用地等,各类用地产值成本投入均有所不同,与此同时,还存在区域自然地理条件,经济发展水平不一致产生的影响,实际补偿价格存在较大差别。农地单位年产值一般几千元,设施农业要高些,若假设存在一个农地市场,将商业、住宅、工业、综合以及农业各类土地置入市场考察,在不改变农地用途前提下可以判断与其他用地价格比较是最低的,农产品价格低,农地产出价值就低,最终导致农地价格低。就各类农地价格单纯比较,受自然条件、土地等级、种植内容、农地投入等等因素影响也存在一定差异。近年在不同线别城市涉及到的城中村改制项目,制定了不同的较高的补偿水平,但总体上特别是在经济欠发达地区农地因各类建设项目被征用后,所得补偿不够保证农民失地后的较稳定生活保障。
政府将所征农地转作新用途后的土地价格都高于农地,这样通过出让(划拨除外)就可获取较高的土地增值收益,而为追求这种收益,政府会尽可能多的征地出让,当然为发展经济征地是必须的,但出现了“土地财政”现象并逐渐形成了恶性循环,其结果是减少了宝贵的耕地,使得逼近十八亿亩耕地红线距离时间缩短,也令大量失地农民谋求到城镇就业,这又增大了城镇建设用地需求,但从另一角度看,国家大量基础设施建设规模逐渐扩大,城镇化又是一个趋势,因次即使不存在“土地财政”农地征用也会继续下去,当然有些征地是用于公益事业。
显然在农地征用货币补偿方面,给出一个适当合理的量化方法具有积极的现实意义,由此我们偿试运用金融衍生工具的期权定价原理,建立征用农地的期权价格补偿模型。
二、期权概念及基本模型
期权是这样一种权利,期权合约持有人在规定时间到期日,有权利但不负有义务(可以但不是必须)按事先约定的价格买进或卖出某项标的资产,标的资产可以是股票,利率、汇率、股票指数等金融类产品,称金融期权,也可以是粮棉豆类农产品、能源、金属矿产品等称作商品期权。期权与期货合约不同点在于:期货合约持有人同样是在规定时间到期日按约定价格买进或卖出标的资产,这种交易无论届时赢损如何双方都必须实施交易,双方权利义务是对等的,而期权交易的双方权利义务是不对等的,期权交易的多头方可以视对自己是否有利决定实施或者不实施,即到时有权买进或卖出或放弃交易,为了获取这种可以选择的权利,签约时多头方应支付一定数量的期权金,(期货没有支付)。如果期权合约持有人获得在到期日按约定价格买入某项标的资产权利,称作买方期权(看涨期权)。简称买权。持有这种权利在到期日资产价格高于约定价格就可以实施买权,否则就放弃这一买权,例如,合约中的标的资产是某支股票期限一年,约定价格50元,现在股价是48元,若一年后股价上升到55元,则实施买权,按约定价格50元买进,权利人赢利55-50=5元,(暂不考虑期权金因素),若到期时股价为49元或更低,则权利人放弃该项买权以避免更大损失。与买权对应的是若期权合约持有人在到期日有权卖出某项标的资产,称为卖方期权(看跌期权)简称卖权,仍以股票为例,设约定价格50元,签约时股价51元,在到期日,股价下落至48元,则权利人实施卖权,按50元卖出,获利50-48=2元,(不考虑期权金因素),如果在到期日股价为52元,则放弃卖权。当然若获得买权或卖权,必须支付一定数量期权金,称买权多头和卖权多头,与之对应的合约另一方称买权空头和卖权空头,设约定价格为K,到期日时标的资产价格为ST.如果执行期权,则
买权收益=ST-K
卖权收益=K-ST
考虑到已支付的期权金,实际收益小于上述表达式,而放弃权利不执行,多头方则仅损失所支付的期权金。
那么期权合约签约时标的资产价格SO是知道的,但到期日的价格ST是未知的,损益也是不确定的,应当支付的期权金是多少,也就是买权和卖权的价格是多少?自然涉及对期权的定价,在假设标的资产价格变动遵循几何布朗运动的前提下,得出刻画期权价格变化的偏微分方程-————Black-Scholes方程:(简称BS方程)
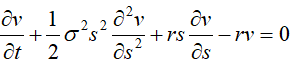 …………(1) …………(1)
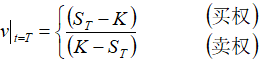 ………… (2)
………… (2)
0≤S<∞ 0≤t≤T
最终得到买权价格定价公式:
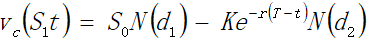 ………………(3) ………………(3)
卖权价格定价公式:
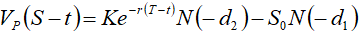 ……………(4) ……………(4)
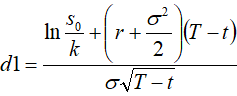 ……………………(5)
……………………(5)
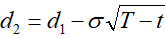 ……………………(6)
……………………(6)
式中:SO是签约时(t=0)的标的资产价格,K是约定价格(期权执行价格),r是无风险利率,T是期限,t是期权签约后经过的时间变量,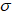 2是标的资产价格变动的方差(由标的资产价格历史数据统计得出),N(.)是正态累积概率。 2是标的资产价格变动的方差(由标的资产价格历史数据统计得出),N(.)是正态累积概率。
由于上述期权合约有确定的期限T,并且多头方只能在期满时才可以决定是否执行,具有这种特征的期权称欧式期权,BS定价公式是针对欧式期权的,除此之外,根据期权合约具体条款的不同,还有标的资产在期限内有无特殊人为干扰(比如支付股利、资源开采减少储量等),在BS模型基础上,还可以给出扩展的及其它种类期权定价公式。
三、美式期权
有一种与欧式期权不同类型的期权,这就是美式期权,其特征是,权利人在0<t≤T内的任一时间点随时可以行使权利,而欧式期权则只能在t=T时的期权到期日才能行使权利美式期权没有类似欧式期权的价格显式表达,不过已有分析得出的结论是,当标的资产是不支付股利的股票时,美式买权提前实施是不明智的,因而可以用BS公式定价。对美式卖权而言,当标的资产下跌到一定程度时提前执行卖权是必要的,否则将蒙受损失,进一步有:
(一)继续持有区域Σ1,在Σ1内,美式期权价格大于期权收益,期权多头不应执行权利,称Σ1 为继续持有区域。
(二)终止持有区域Σ2,
在该区域,期权期望收益率小于无风险利率,应立即执行期权终止合约,称终止持有区域。
(三)由于美式期权可以提前实施,期权多头就拥有比欧式期权更多的获利机会,因此它比欧式期权价格更高,在参量相同条件下,美式期权价格至少不低于欧式期权价格。
美式期权定价可以分解成两部:一部分是欧式期权价格,另一部分是提前实施条款所应增付的期权金,这一增加部分与最佳实施边界位置有关,涉及难以求解的非线性积分,因而美式期权定价不能给出显式解析表达。
四、征地补偿的期权属性识别分析
BS期权定价模型除应用于金融领域外,其方法原理逐渐被引入到实物资产,权益类资产及项目等价值评估业务领域,并有着很好的实践应用案例,例如知识产权类价值评估是涉及买权,股权价值评估对流动性缺乏折扣的期权模型、保险租赁以及人力资源评估则涉及到卖权,运用期权原理给资产定价除了要能够识别出项目资产具有的内嵌期权特性外,还需对BS模型中的参量实施变通处理,一般情形对照见下表:
|
金融期权(以股票为例)
|
实物期权
|
|
股票当前价格SO
|
项目资产运营产生的现金流现值
|
|
执行价格K
|
投资成本和运营成本现值
|
|
到期时间T
|
项目运营存续时间
|
|
股票价格的不确定性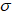 2 2
|
资产价值或现金流的不确定性
|
|
无风险利率r
|
无风险利率r
|
|
股利支付率β
|
自然资源价值生产消耗率
|
在市场环境所决定的经济活动中,所面临的项目资产内容,性质、目的比较复杂,必须具体加以分析判断,确定是买权还是卖权以及各参量,一个农业方面具有期权属性的例子是关于国家农产品收购牌价的制订,当某种重要农产品的市场需求相对于供给增长更快时其市场价格可能会高于收购价,生产者就会到市场出售,反之就出售给国家,这种收购牌价类似于卖权约定价格,而这一卖权是国家(政府)无偿赋予农户的,无需支付费用,主要目的是保护种植积极性,稳定一些重要农产品的生产和供应,这种卖权在单一计划经济中是不存在的,现以小麦为例,计算这一卖权价值。
假设今年市场6月份小麦价格1.2元/斤,国家公布的次年6月份开始有效的小麦收购牌价1.3元/斤,具体参量如下:
SO=j=1.3
T=1 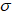 2=0.023 2=0.023 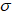 =0.15
r=0.05 =0.15
r=0.05
(b的值据前十年左右小麦市场价格数据计算),代入BS公式:
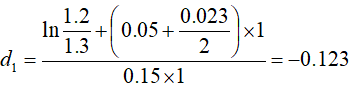
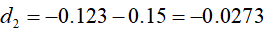
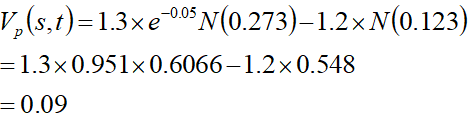
我们得出了这样一个卖权的价值是每斤小麦0.09元,即每百斤小麦9元,以每亩小麦产量1000斤计算,国家收购牌价相当于每亩小麦提供了“保险费”价值90元。
现在回到征地补偿上,政府征用农地后是要改变用途的,对于转为建设用地,存在着一个市场价格,并且一般都高于农地价格,农地使用权、承包权、经营权流转市场完全不同于非农地土地市场,政府征地并补偿后农民失去一切土地权利,政府所征土地性质转为国有土地使用权的建设用地,或者用于国家公共项目用地或用来出让纳入土地市场,此时可以认为:农地所有者天然拥有其土地的一个卖方期权,约定执行价格乃是改变用途后的土地价格。在征地行为发生时,农地所有者有权按约定价格卖出土地资产,或者说,政府欲取得农地所有权,就要买回该卖权,由于征地行为事先不确定,征地一旦发生,意味着同时将会执行卖权,显然这类似一个美式期权,问题是美式期权毕竟有一个长度T时间段的约束。
值得庆幸的是,有一种美式期权恰恰没有终止期的约束,期权价格与时间无关,在T-∞的区间任一时点上均可以实施权利,具有这样特征的美式期权称作永久美式期权,我们虚拟征用农地所嵌卖权完全符合这一期权特征,是一个永久美式期权的卖权价格定价问题,而永久美式期权价格存在显式表达,解决了征地补偿定量问题。
五、征地补偿期权价格定量分析
刻画欧式期权价格变化的BS方程如前述(1)式形如:
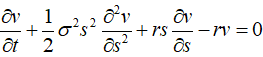 这是一个偏微分方程,而永久美式期权与时间变量t无关,删去对t的微分项就得到: 这是一个偏微分方程,而永久美式期权与时间变量t无关,删去对t的微分项就得到:
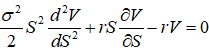 …………………………(7) …………………………(7)
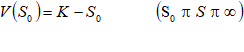 …………………………(8) …………………………(8)
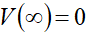 …………………………(9)
…………………………(9)
SO是最佳实施边界,征地行为一旦发生,就认为永久美式卖权 的执行条件具备了,但SO是未知的,定解问题(7)-(9)是一个给定在(SO ∞)上的二阶常微分方程边值问题。
作变量代换V=Sβ
有: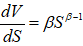 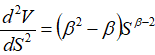
代入(7)式:
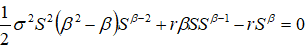
整理得: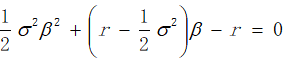
关于β的二次方程有两个根:

方程式(7)的通解为:
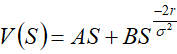 …………………(10)
…………………(10)
再利用边界条件(8)(9)给出A B
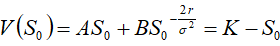 …………………(1)’
…………………(1)’
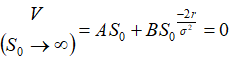 …………………(2)’ …………………(2)’
由(2)’得出A=0,代入(1)’得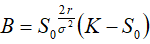 代入(10)式,得出定解问题(7)-(9)的解: 代入(10)式,得出定解问题(7)-(9)的解:
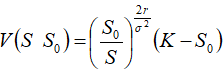 …………………(11)
…………………(11)
根据前面的讨论,当标的资产价格S=SO时,永久美式期权收益达到极大值,此时该卖权价格与实施期权后的收益相等
即: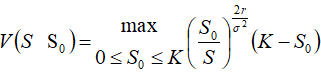 ,为求SO,对(11)式求关于SO的一阶导数,并令其等于0 ,为求SO,对(11)式求关于SO的一阶导数,并令其等于0
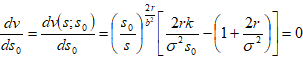
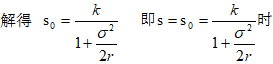
农地卖权价格最大,并且等于期望收益:
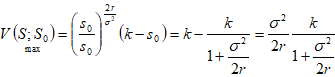 …………………(12) …………………(12)
此时征地方和被征地方也就是卖权空头和卖权多头双方体现了一种平衡结果。
六、进一步的讨论
式(12)即为征用农地补偿价格表达式,只有三个参量K, 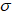 2,r,显得很简洁。 2,r,显得很简洁。
(一)K是卖权执行价格(约定价格),它是所征农地转作它用的市场价格,这是一个虚拟过程,但执行价格却是一个实实在在重要的量,我们注意到在表达式中农地价格并不存在,仅依赖新用途后的地价,显然不够全面反映农地实际情况而有所欠缺,故应当结合所征农地的产值、位置、等级诸多因素综合考虑,特别是国家用以高铁、高速公路、基础水利设施建设用地,在现有土地市场没有相关价格反映,更需合理确定K值,最佳实施边界S0并不是实施卖权时真正意义上的最小农地价格,只是通过解析过程得出的一个表征性参量。
(二)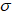 2是征地后新用途土地的市场价格变动的方差,可以依据征地地区前若干年同类用途地价统计得到,若采集到一定时期的地价是K0、K1、K2……Kn 则: 2是征地后新用途土地的市场价格变动的方差,可以依据征地地区前若干年同类用途地价统计得到,若采集到一定时期的地价是K0、K1、K2……Kn 则:
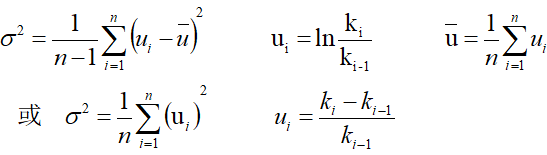 (三)r是无风险利率,可以选择银行存款利率或国债利率,究竟用短期还是长期利率尚需讨论,对没有时间限定的美式永久期权并且是土地资产而言,似乎用长期利率为宜。 (三)r是无风险利率,可以选择银行存款利率或国债利率,究竟用短期还是长期利率尚需讨论,对没有时间限定的美式永久期权并且是土地资产而言,似乎用长期利率为宜。
上述三个参量K、 2、r与卖权价格 2、r与卖权价格
V(S;S0)是怎样的函数关系属性也是有意义的,具体分析如下:
a、对(12)式 求K的一阶偏导数:
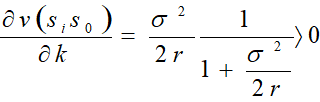
可知表达式是K的增函数,即随着K的增大,补偿价格随之增高,这一点对卖权多头是显而易见的。
b、对(12)式求 2的一阶偏导数: 2的一阶偏导数:
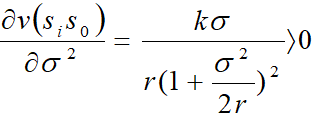
即补偿价格是土地价格变动方差的增函数,关于这一点的解释是,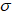 2高表明土地价格变动比较剧烈,对永久美式期权的多头来说,能够较易捕捉到最佳实施的时机增加了,加大了获得最高收益的概率。 2高表明土地价格变动比较剧烈,对永久美式期权的多头来说,能够较易捕捉到最佳实施的时机增加了,加大了获得最高收益的概率。
对(12)式求关于r的偏导数:
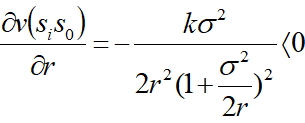
可知补偿价格是无风险利率r的减函数,即随r的增大,补偿价格减少,其解释是由于是卖权,且等待执行的机会可能会很长,从卖出卖权获得现金补偿,无风险利率使受偿者损失掉一部分资金时间价值,利率高,损失掉的时间价值也高。
第一个假想案例:
设修建高速公路,需用某县某村部分农地,根据农地的等级,位置及产值等因素综合分析,确定所征地与该县最末级工业用地价格较为适应,每亩9万元,该类工业地价近几年价格变动的方差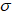 2为10%,无风险利率3%,将上述参量代入(12)式: 2为10%,无风险利率3%,将上述参量代入(12)式:
每亩补偿价格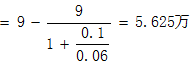
第二个假想案例:
设某省会城市开发大型绿地项目,需整村征用城中村土地,由于不是商业开发,而是公益性的,此时的执行价格K不能用商、住等用途地价来确定,可以考虑用该城市的一个各类用途综合平均地价做为执行价格,若这个综合平均地价为200万/亩,综合地价波动的方差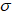 2=12%
, 无风险利率r=4% 2=12%
, 无风险利率r=4%
征地价格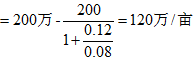
综合地价波动率以各用途地价波动率和各地价所占比重加权: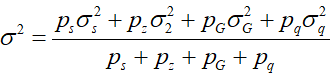
PS、Pz、PG、Pq分别是商业、住宅、工业其它用途各自平均地价,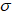 2S、 2S、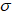 2z、 2z、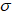 2G、 2G、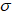 2q分别是各用途地价变动的方差。 2q分别是各用途地价变动的方差。
若单独分离城中村宅基地进行补偿,则执行价格采用城市住宅地价,可参考该城中村周边住宅地价,设最终确定的住宅地价为800万/亩,价格波动的方差是15%,无风险利率4%,则宅基地补偿价格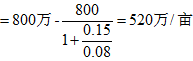
七、扩展的征地价格期权补偿模型
当模型中标的资产比如股票存在支付股利的情形,设经过换算后的年股利支付率为q,它的存在将导致股票价格降低,就买权而言,执行价格K是固定的,期权执行时的收益
S-K将会减少,从而令期权价格降低,对卖权来说,情况恰恰相反,即随q的存在,卖权期权价格会增大。
具体到标的资产是土地时,什么样的情形会令土地价值或价格减少,我们考虑以下因素:
(一)由于工业性污染造成的减产损失。
(二)由于工业性污染造成农产品品质降低而影响到产品价格降低之损失。
(三)为消除污染使土地恢复至正常条件额外投入的费用。
(四)阻滞土地荒漠化趋势需投入的资金。
(五)为防止土地地力过速下降而投入的费用。
上述因素可量化为类似股票支付股利,设正常情况下农地年产值为Ld,针对上述因素(不一定同时作用)1、2项q=损失/Ld,3、4、5项q=费用/Ld。
当模型引入q时,(7)式变为: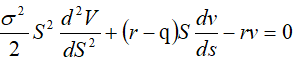 ………………(13)
………………(13)
(S0<S<∞)
V(S0)=K-S0
……………………………………………(14)
V(∞)=0 ………………………………………………(15)
同样取变量代换:V=Sa,最终解得使期权价格最大的
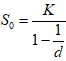 ………………………………………………(16) ………………………………………………(16)
则: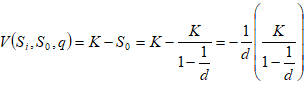 ……………(17) ……………(17)
其中:
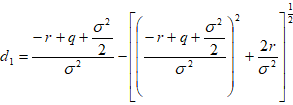 ………………(18) ………………(18)
现仍沿用第一假想案例,其它参量不变只是增加q=0.05,用(18)式:
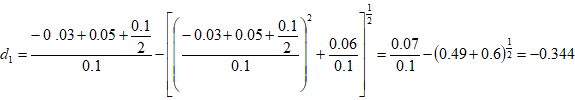 再利用(17)式: 再利用(17)式:
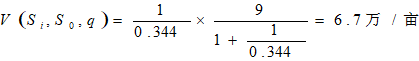
结果比没有类似股利支付的土地价值降低率时,补偿价格高出1万,现实中当利用未扩展模型计算补偿仍显不足且存在对农地价值降低影响因素,可考虑采用扩展模型。
八、结束语
目前我国农地市场尚未实际开放,发育成度远远低于其它用地市场,保证粮食安全是国家制定的一项基本国策,对农地的管理极其严格,不可能形成真正意义上的市场,但是一旦改变了农地用途后,将其置入土地市场来考察就存在着合理性,我们利用征地行为中内嵌的具有期权的一些特性,通过在一个期权市场机理下的模拟过程得出补偿模型,而并非实质和真正意义上的期权衍生品交易结果,随着我国市场经济发展的深入和不断完善,针对参考农地产出价值确定征地补偿价格和参考改变用途后的土地市场价格确定补偿价格,后者似乎为克服前者具有的不适应性提供了一种思路和方法。
参考文献:姜礼尚.2003. 期权定价的数学模型和方法【M】.北京:高等教育出版社
|
